Adaptation of a trait to different optima in different demes

Show code cell source Hide code cell source

import fwdpy11
import demes
import demesdraw
import numpy as np

First, set up some basic parameters that we will need:

# diploid population size:
N=1000
genome_length=1e8

We will simulate a simple model of a population split:

yaml=f"""
time_units: generations
demes:
 - name: ancestor
   epochs:
    - end_time: 100
      start_size: {N}
 - name: deme0
   ancestors: [ancestor]
   epochs:
    - start_size: {N}
 - name: deme1
   ancestors: [ancestor]
   epochs:
    - start_size: {N}
"""

demesdraw.tubes(demes.loads(yaml));

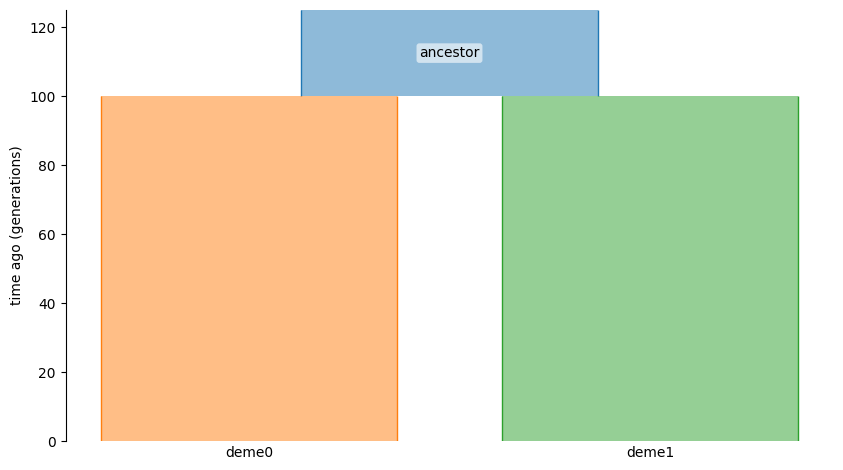
There are three demes in this model: the ancestor and the two descendants. We want to have each descendant deme evolve to a different phenotypic optimum. To do this, we must supply a genetic value calculation for each of the three demes in the model:

optima_ancestor = [fwdpy11.Optimum(when=0, VS=1.0, optimum=0.0)]
optima_deme0 = [fwdpy11.Optimum(when=0, VS=1.0, optimum=0.0),
                fwdpy11.Optimum(when=10*N, VS=1.0, optimum=1.0)
                ]
optima_deme1 = [fwdpy11.Optimum(when=0, VS=1.0, optimum=0.0),
                fwdpy11.Optimum(when=10*N, VS=1.0, optimum=-1.0)
                ]
gss_ancestor = fwdpy11.GaussianStabilizingSelection.single_trait(optima=optima_ancestor)
gss0 = fwdpy11.GaussianStabilizingSelection.single_trait(optima=optima_deme0)
gss1 = fwdpy11.GaussianStabilizingSelection.single_trait(optima=optima_deme1)

We will model additive effects on the trait:

gvalue = [fwdpy11.Additive(scaling=2.0, gvalue_to_fitness=gss_ancestor),
          fwdpy11.Additive(scaling=2.0, gvalue_to_fitness=gss0),
          fwdpy11.Additive(scaling=2.0, gvalue_to_fitness=gss1)]

We will model effect sizes as constant across demes. We can use fwdpy11.GaussianS to model a Gaussian distribution of effect sizes:

dfe = fwdpy11.GaussianS(0, genome_length, 1.0, sd=0.1)

The rest of the setup is straightforward. We will evolve the population and print out the final mean trait values, which will be very close to the optima of each descendant deme.

Show code cell source Hide code cell source

demog = fwdpy11.ForwardDemesGraph.from_demes(yaml, burnin=10)
pdict = {
    'sregions': [dfe],
    'recregions': [fwdpy11.BinomialInterval(0, genome_length, 0.5)],
    'rates': (0, 5e-3, None),
    'demography': demog,
    'gvalue': gvalue,
    'simlen': 10*N + 100,
    'prune_selected': False,
}
params = fwdpy11.ModelParams(**pdict)
pop = fwdpy11.DiploidPopulation(N, genome_length)
rng = fwdpy11.GSLrng(54321)
fwdpy11.evolvets(rng, pop, params, simplification_interval=100)
md = np.array(pop.diploid_metadata)
for deme in np.unique(md["deme"]):
    w = np.where(md["deme"] == deme)
    print(f"mean trait value in deme {deme} = {md["g"][w].mean()}")

mean trait value in deme 1 = 0.9288320707795822
mean trait value in deme 2 = -1.0138504399491264

To see how to extend this model to allow the effect sizes to differ across demes, see here.